第4回深層学習による画像分類

今回のテーマは深層学習による画像分類で、深層ニューラルネットワークを使用して犬と猫の画像の分類を行います。

今回は深層ニューラルネットワークの中でも特に畳み込みニューラルネットワーク(以下CNN)と呼ばれる、画像系のタスクによく用いられるニューラルネットワークを使用します。

CNNの概要については解説動画をご覧ください。また、今回はアルゴリズムセミナーとなっているため、実際にモデルを構築して学習・評価を行います。

今回の実装のソースコードはこちらからダウンロードできます。

解説動画

実装概要

TensorFlow、Kerasを用い、CNNのモデルの１つであるVGG16を転移学習させて、犬と猫の画像の分類を行います。

機械学習フレームワーク

今回使用するTensorFlow、Kerasは機械学習フレームワークです。機械学習フレームワークを使用することで、機械学習に必要なコードを簡略化し、モデルの作成や学習などを簡単に行うことができます。また、学習済みモデルを提供しているのでそれを呼び出して使うこともできます。

機械学習フレームワークの例

scikit-learn (https://scikit-learn.org/)
- Pythonのオープンソース機械学習ライブラリ
- 初版は2007年に公開
TensorFlow (https://www.tensorflow.org/)
- Googleが2015年11月に公開
Keras (https://keras.io/)
- François Cholletが2015年3月27日に公開
- 現在はTensorFlowに統合されている。
  - tf.Keras(https://www.tensorflow.org/guide/keras?hl=ja)
  - 今回使用するKerasはこちら
PyTorch (https://pytorch.org/)
- FacebookのTorchが元。2016年に公開

実装の流れ

1. データセットの準備

モデルを構築する前にまず学習に用いるデータセットを準備します。ここではデータセットのダウンロードと、学習に適した形式への整理を行います。

2. 学習の準備

学習の前に学習条件の設定とKerasのImageDataGeneratorを用いてGenerator(※詳細は後述)の作成をします。

3. 学習

モデルの構築、学習の実行を行います。

4. 評価

学習したモデルを用いて評価データに対する予測を行い、予測値を評価します。

実装

Google Colaboratory

以下の実装では前回同様Google Colaboratoryを使用します。※実行にはGoogleアカウントが必要となります。

今回はGPUを使用するため、ランタイムのタイプをGPUに設定します。
画面上部の「ランタイム」→「ランタイムのタイプを変更」→「ハードウェアアクセラレータ」のNoneをGPUに変更し、保存します。

データセットの準備

データセットのダウンロード・解凍

公開されたGoogle Driveからデータセットをダウンロードし、zipを解凍します。

参考 https://github.com/GitHub30/gdrive.sh

# 画像ファイルをダウンロード
!curl gdrive.sh | bash -s 1iuDqJ5QewZ0J26eCfJk3-Xbp1nnjKm3o

  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100  2874  100  2874    0     0   3565      0 --:--:-- --:--:-- --:--:--  3570
  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100  3281    0  3281    0     0   8964      0 --:--:-- --:--:-- --:--:--  8940
  % Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
                                 Dload  Upload   Total   Spent    Left  Speed
100   408    0   408    0     0   1714      0 --:--:-- --:--:-- --:--:--  1714
  0     0    0     0    0     0      0      0 --:--:-- --:--:-- --:--:--     0
  0     0    0     0    0     0      0      0 --:--:-- --:--:-- --:--:--     0
100 94.1M  100 94.1M    0     0  36.7M      0  0:00:02  0:00:02 --:--:-- 88.2M
curl: Saved to filename 'train.zip'

# ファイルを解凍
!unzip /content/train.zip > /dev/null

trainディレクトリが作成されればOKです。

※ファイル数が多いため、trainディレクトリを開くとフリーズしてしまうことがあります。

画像データの確認

解凍されたら画像を確認します。

# ライブラリのインポート(globライブラリを用いてファイル検索)
import glob

# ファイル一覧を取得
images = glob.glob('/content/train/*.jpg')

# ファイル名を確認(先頭3枚)
print(images[:3])

['/content/train/dog.152.jpg', '/content/train/dog.767.jpg', '/content/train/dog.296.jpg']

# 画像表示に必要なモジュールをインポート
import matplotlib.pyplot as plt
from PIL import Image

# 画像の表示
image_sample = images[0]
img = Image.open(image_sample)
print('filename:{}, size:{}'.format(image_sample, img.size))
plt.imshow(img)
plt.show()

filename:/content/train/dog.152.jpg , size:(500, 499)

※乱数シードを固定していないので、表示される結果が異なる場合があります。

画像データセットの分割

データセットを学習データ(train)、検証データ(val)、評価データ(test)に分割します。train、val、testの割合は16:4:5とします。
※全データをtrain+valとtestに8:2で分けた後、さらにtrainとvalを8:2で分けるため、このような割合になります。

ここではKerasで学習できるよう犬と猫の画像ファイル(計3000枚)を以下のディレクトリ構成で配置します。

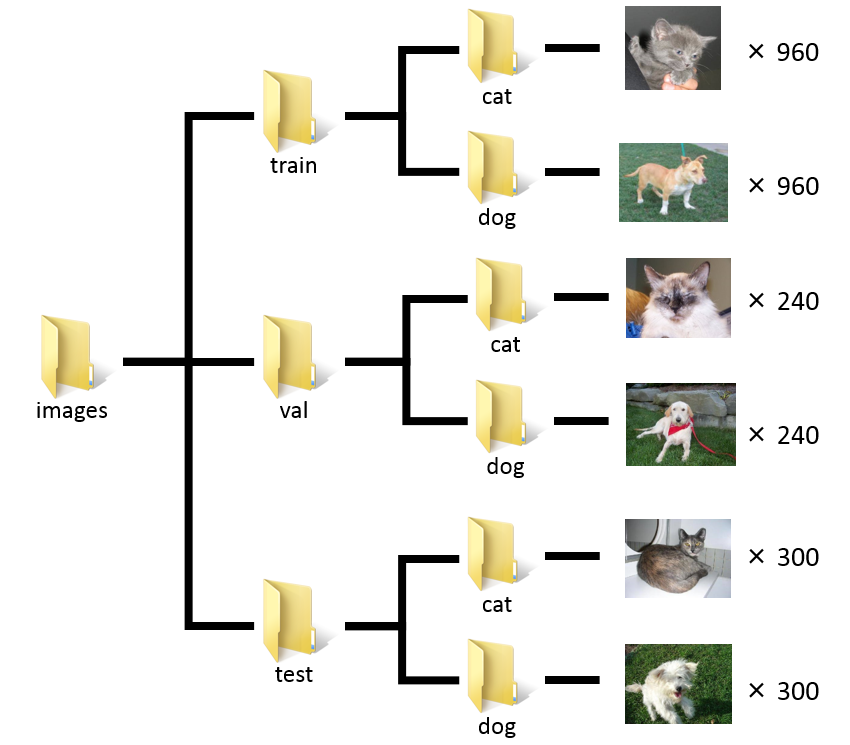
train、 val、 testのそれぞれの用途は下記の通りです。

train … 実際にモデルのパラメータを更新するための学習データ。
val(validation) … 学習の途中でモデルの良し悪しを確かめるための検証データ。パラメータの更新には用いない。
test … 学習後にモデルの予測精度を確かめるための評価データ。パラメータの更新には用いない。

import os 

# train用フォルダ作成
os.makedirs('/content/images/train/dog', exist_ok=True)
os.makedirs('/content/images/train/cat', exist_ok=True)

# val用フォルダ作成
os.makedirs('/content/images/val/dog', exist_ok=True)
os.makedirs('/content/images/val/cat', exist_ok=True)

# test用フォルダ作成
os.makedirs('/content/images/test/dog', exist_ok=True)
os.makedirs('/content/images/test/cat', exist_ok=True)

# 犬・猫ごとのファイルパス一覧を取得
images_dog = glob.glob('/content/train/dog.*.jpg')
images_cat = glob.glob('/content/train/cat.*.jpg')

# ファイルを分割(train, val, test)
idx_test_start = int(len(images_cat) * 0.8)
idx_val_start = int(idx_test_start * 0.8)

images_train_dog = images_dog[:idx_val_start]
images_train_cat = images_cat[:idx_val_start]

images_val_dog = images_dog[idx_val_start:idx_test_start]
images_val_cat = images_cat[idx_val_start:idx_test_start]

images_test_dog = images_dog[idx_test_start:]
images_test_cat = images_cat[idx_test_start:]

import shutil

# 一括でファイルを移動する関数を作成
def move_files(file_list, target_dir):
    for file in file_list:
        shutil.move(file, target_dir)

# ファイル移動
move_files(images_train_dog, '/content/images/train/dog/')
move_files(images_train_cat, '/content/images/train/cat/')
move_files(images_val_dog, '/content/images/val/dog/')
move_files(images_val_cat, '/content/images/val/cat/')
move_files(images_test_dog, '/content/images/test/dog/')
move_files(images_test_cat, '/content/images/test/cat/')

学習の準備

学習条件設定

学習の準備として、学習の条件を下表の値で設定します。

変数名	設定値	意味
classes	[‘cat’, ‘dog’]	分類するクラスのリスト
train_data_dir	‘images/train’	学習データのディレクトリ
validation_data_dir	‘images/val’	検証データのディレクトリ
test_data_dir	‘images/test’	評価データのディレクトリ
epochs	10	エポック数(全データを学習する回数)
batch_size	16	バッチサイズ(1ステップで学習する画像の枚数)
img_width	224	入力層の画像の幅
img_height	224	入力層の画像の高さ

ここで、エポック数とバッチサイズについて補足しておきます。

学習は各データを順番に入力しモデルのパラメータを更新していくのですが、このとき全ての学習データを一通り使用した状態を1エポックといい、この1サイクルを回した回数をエポック数といいます。今回はエポック数10なので10回サイクルを回すということです。

また、一般的に1回のパラメータの更新はいくつかのデータをまとめて入力して行いますが、このときまとめて入力するデータ数のことをバッチサイズといいます。今回バッチサイズが16なので16枚の画像をまとめて入力するということです。

#分類するクラス
classes = ['cat', 'dog']
nb_classes = len(classes)
 
# データのディレクトリ
train_data_dir = '/content/images/train'
validation_data_dir = '/content/images/val'
test_data_dir = '/content/images/test'

# 学習回数
epochs = 10

# バッチサイズ
batch_size = 16

# 画像サイズ
img_width, img_height = 224, 224

ImageDataGeneratorの作成

train、val、testデータそれぞれのImageDataGeneratorを作成します。

ImageDataGeneratorとは何かというと、データの合計サイズが小さい場合はデータを一括でメモリに読み込ませますが、大きい場合はメモリにデータが乗り切らない場合があるためそうはいきません。そのため、画像の読み込みを一括ではなく、逐次的に行い、メモリ負荷を軽減することができるのがImageDataGeneratorです。ImageDataGeneratorはKerasのモジュールとして用意されているので、それをそのまま使用します。

また、今回は使用しませんが、元データを加工してそれをデータセットに加えることでデータのバリエーションを増やす、データ拡張の機能もImageDataGeneratorは持っています。

from tensorflow.keras.preprocessing.image import ImageDataGenerator

# 学習データのImageDataGenerator作成
train_datagen = ImageDataGenerator(rescale=1.0 / 255)  # rescaleで各画素のスケールを0～255から0～1に変換
train_generator = train_datagen.flow_from_directory(
    directory=train_data_dir,
    target_size=(img_width, img_height),
    color_mode='rgb',
    classes=classes,
    class_mode='categorical',
    batch_size=batch_size
)

Found 1920 images belonging to 2 classes.

# 検証データのImageDataGenerator作成
validation_datagen = ImageDataGenerator(rescale=1.0 / 255) 
validation_generator = validation_datagen.flow_from_directory(
    directory=validation_data_dir,
    target_size=(img_width, img_height),
    color_mode='rgb',
    classes=classes,
    class_mode='categorical',
    batch_size=batch_size
)

Found 480 images belonging to 2 classes.

評価データは学習後に予測値と正解ラベルと照らし合わせるため、データをシャッフルしないようにshuffle=Falseとします。

# 評価データのImageDataGenerator作成
test_datagen = ImageDataGenerator(rescale=1.0 / 255) 
test_generator = test_datagen.flow_from_directory(
    directory=test_data_dir,
    target_size=(img_width, img_height),
    color_mode='rgb',
    classes=classes,
    class_mode='categorical',
    shuffle=False  # シャッフルしない
)

Found 600 images belonging to 2 classes.

学習

学習はVGG16を転移学習させて行います。

学習済みモデル

学習済みモデルVGG16を読み込みます。
最終層は差し替えるため、include_top=Falseと指定して読み込まないようにします。

from tensorflow.keras.applications.vgg16 import VGG16
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Input, Flatten, Dense

input_tensor = Input(shape=(img_width, img_height, 3))
VGG16 = VGG16(include_top=False, weights='imagenet', input_tensor=input_tensor)

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/vgg16/vgg16_weights_tf_dim_ordering_tf_kernels_notop.h5
58892288/58889256 [==============================] - 1s 0us/step
58900480/58889256 [==============================] - 1s 0us/step

モデルの作成

転移学習を行うため、VGG16のパラメータは凍結し、最終層に全結合層を追加します。

# VGG16のパラメータを凍結(すべての層を凍結)
for layer in VGG16.layers:
    layer.trainable = False

# 差し替え用の新しい層を追加
model = Sequential()
model.add(VGG16)
model.add(Flatten())
model.add(Dense(nb_classes, activation='softmax'))

model.summary()を実行すると、構築したモデルの概要が表示されます。

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                Output Shape               Param #
=================================================================
vgg16 (Functional)          (None, 7, 7, 512)          14714688
flatten (Flatten)           (None, 25088)              0
dense (Dense)               (None, 2)                  50178
=================================================================
Total params: 14,764,866
Trainable params: 50,178
Non-trainable params: 14,714,688
_________________________________________________________________

modelに追加した各層(Layer)の出力形状(Output Shape)とパラメータ数(Param #)が追加した順に表示されています。また、VGG16のパラメータは凍結したため、学習可能パラメータ数(Trainable params)は全結合層だけの50,178となっています。

モデルをコンパイルして学習方法を設定します。ここでは損失関数(loss)にクロスエントロピー、最適化アルゴリズム(optimizer)にAdam、学習中の評価指標(metrics)にaccuracyを用いるように設定します。

from tensorflow.keras import optimizers

model.compile(loss='categorical_crossentropy',
              optimizer=optimizers.Adam(learning_rate=1e-3),
              metrics=['accuracy'])

学習の実行

いよいよ学習を実行します。学習はmodel.fit()で行います。fit()の引数には学習データとステップ数、エポック数、そして検証データを渡します。
ステップ数とは、1エポックあたり何回パラメータの更新を行うかを表す数で、全データ数 / バッチサイズで与えられます。

historyにmodel.fit()の戻り値を渡しているのは、後で学習の経過をグラフで確認するためです。

# 学習
steps_per_epoch = int(len(train_generator.classes) / batch_size) 
history = model.fit(
    x=train_generator,  # 学習データ
    steps_per_epoch=steps_per_epoch,  # ステップ数
    epochs=epochs,  # エポック数
    validation_data=validation_generator  # 検証データ
)

Epoch 1/10 120/120 [==============================] - 33s 163ms/step - loss: 0.4411 - accuracy: 0.8448 - val_loss: 0.6074 - val_accuracy: 0.7625
Epoch 2/10 120/120 [==============================] - 20s 162ms/step - loss: 0.1866 - accuracy: 0.9292 - val_loss: 0.2675 - val_accuracy: 0.9083
Epoch 3/10 120/120 [==============================] - 20s 164ms/step - loss: 0.0580 - accuracy: 0.9807 - val_loss: 0.3137 - val_accuracy: 0.8771
Epoch 4/10 120/120 [==============================] - 20s 165ms/step - loss: 0.0258 - accuracy: 0.9979 - val_loss: 0.2270 - val_accuracy: 0.9167
Epoch 5/10 120/120 [==============================] - 20s 166ms/step - loss: 0.0147 - accuracy: 1.0000 - val_loss: 0.2280 - val_accuracy: 0.9167
Epoch 6/10 120/120 [==============================] - 20s 164ms/step - loss: 0.0114 - accuracy: 1.0000 - val_loss: 0.2470 - val_accuracy: 0.9208
Epoch 7/10 120/120 [==============================] - 20s 163ms/step - loss: 0.0090 - accuracy: 1.0000 - val_loss: 0.2378 - val_accuracy: 0.9187
Epoch 8/10 120/120 [==============================] - 20s 163ms/step - loss: 0.0069 - accuracy: 1.0000 - val_loss: 0.2604 - val_accuracy: 0.9187
Epoch 9/10 120/120 [==============================] - 20s 163ms/step - loss: 0.0063 - accuracy: 1.0000 - val_loss: 0.2390 - val_accuracy: 0.9167
Epoch 10/10 120/120 [==============================] - 20s 163ms/step - loss: 0.0050 - accuracy: 1.0000 - val_loss: 0.2417 - val_accuracy: 0.9104

先ほどエポック数を10と設定したため、10エポック分学習しました。結果は各エポックごとに出力されており、それぞれの出力結果の各項目の説明は以下のとおりです。

loss … 学習データで予測した場合の損失関数
accuracy … 学習データにて、正しく予測できた画像数の割合
val_loss … 検証データで予測した場合の損失関数
val_accuracy … 検証データにて、正しく予測できた画像数の割合

10エポック目での値を見ると、学習データでのaccuracyが1と非常に高く、検証データでのaccuracyは0.9104となかなかの結果となりました。

では学習の経過はどうなっているでしょうか？分かりやすいように、グラフにプロットしてみます。

# グラフ描画(2画面)
plt.figure(figsize=(8, 4))

# epochごとのlossを表示
plt.subplot(1, 2, 1)
plt.plot(range(1, epochs+1), history.history['loss'], '-o')
plt.plot(range(1, epochs+1), history.history['val_loss'], '-o')
plt.title('loss_transition')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.grid()
plt.legend(['loss', 'val_loss'], loc='best')

# epochごとのaccuracyを表示
plt.subplot(1, 2, 2)
plt.plot(range(1, epochs+1), history.history['accuracy'], '-o')
plt.plot(range(1, epochs+1), history.history['val_accuracy'], '-o')
plt.title('accuracy_transition')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.grid()
plt.legend(['accuracy', 'val_accuracy'], loc='best')

# グラフ表示
plt.show()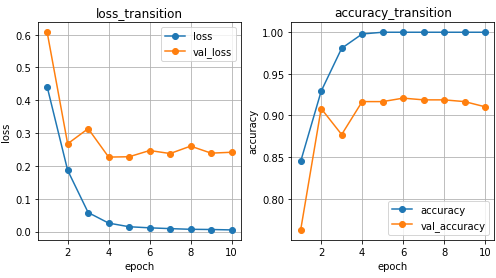

左側のグラフは学習データと検証データそれぞれの、エポックごとのlossの変化を、右側のグラフはエポックごとのaccuracyの変化を表しています。lossは損失関数であり、この値を小さくするように学習しているので、上手く学習が進んでいれば、エポックごとに小さくなっていきます。
これを見ると、学習データのlossは0.005と非常に小さい値に収束していますが、検証データでは4エポック目あたりからやや右肩上がりになっていて、学習が進むごとに精度が悪くなっています。これを過学習といいます。
accuracyについても、学習データのaccuracyは4エポック目でほぼ1となっており、それ以降あまり学習が進んでいないことが分かります。また、検証データの方は6エポック目以降は少しずつaccuracyが下がっていて、過学習の傾向が見られます。

このように、学習のエポックを重ねるうちに過学習してしまうことが多いので、検証データを使って学習途中のlossなどを確認し、検証データのlossが最も低いエポックのパラメータを採用するといった措置を取るのが一般的です。

評価

最後に評価データを使ってモデルの最終的な精度を評価します。

評価データでの予測

model.evaluate(test_generator)で評価データにおけるlossとacuracyが表示されます。

model.evaluate(test_generator)

19/19 [==============================] - 22s 641ms/step - loss: 0.2898 - accuracy: 0.9000
[0.28982675075531006, 0.8999999761581421]

lossが0.2898、accuracyが0.9となりました。

混同行列

次に混同行列を作成してデータを評価します。

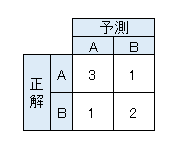
混同行列とは正解と予測の分布を表形式にしたもので、行ごとに正解のクラス、列ごとに予測したクラスが並べられています。

例えば、7枚の画像をAとBの2クラスで分類し、各画像に対して予測と正解が以下のようになった場合を考えます。

予測：[B,A,A,A,B,B,A]
正解：[A,A,A,B,B,B,A]

このとき

Aと予測したもののうち、正解がAだったもの … 3つ
Aと予測したもののうち、正解がBだったもの … 1つ
Bと予測したもののうち、正解がAだったもの … 1つ
Bと予測したもののうち、正解がBだったもの … 2つ

　であるので、混同行列は以下のようになります。

混同行列を作成する前に、評価データの各サンプルに対する正解のラベルと予測したラベルの配列を用意します。

# 正解のラベル一覧を作成。
true = test_generator.classes
true

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1], dtype=int32)

# 予測のラベル一覧を作成
import numpy as np
p = model.predict(test_generator)
pred = np.argmax(p, axis=1)
pred

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
       0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
       1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0,
       0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0,
       0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0,
       0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1,
       1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1,
       1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1,
       1, 1, 0, 1, 1, 1])

ここで0は猫、1は犬のラベルです。

trueとpredが用意できたので、混同行列を表示するTensorFlowのconfusion_matrix()にこれらを渡します。

# 混同行列表示
from tensorflow.math import confusion_matrix
confusion_matrix(true, pred)

<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[268, 32],
       [ 28, 272]], dtype=int32)>

array内の2次元配列が混同行列です。今回の場合、クラスの順番が[cat(猫), dog(犬)]の順のため、混同行列から

猫と予測したもののうち、正解が猫だったもの … 268枚
猫と予測したもののうち、正解が犬だったもの … 28枚
犬と予測したもののうち、正解が猫だったもの … 32枚
犬と予測したもののうち、正解が犬だったもの … 272枚

となったことが分かりました。

補足：その他の評価指標

分類問題ではaccuracyや混同行列以外にも、よく使われる評価指標があります。
代表的なものとしてprecision(適合率)、recall(再現率)、F1(F値)があります。

例えば、クラスAとBの2クラス分類での予測結果に対するAのprecision、recall、F1は以下の式で計算されます。

$$precision(適合率) = \frac{Aと予測したもののうち実際にAだった数}{Aと予測した数}$$ $$recall(再現率) = \frac{Aが正解であるもののうちAと予測した数}{Aが正解である数}$$ $$F1(F値) = 2 \times \frac{precision \times recall}{precision + recall}$$

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score

print('precision:', precision_score(true, pred))
print('recall:', recall_score(true, pred))
print('f1_score:', f1_score(true, pred))

precision: 0.8947368421052632
recall: 0.9066666666666666
f1_score: 0.9006622516556291

※scikit-learnのprecision_score()、recall_score()、f1_score()はデフォルトではラベルが1のクラスのスコアを計算します。つまりここで得られた各指標の値は犬クラスに対するprecision、recall、F1を表しています。

他のラベルについて計算する場合は、例えばprecision_score()などの引数にpos_label=0としてやると、ラベルが0のクラスに対して計算することができます。

参考：https://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_score.html#sklearn.metrics.precision_score

今回はこれで以上になります。次回のテーマは文字認識の予定です。

最後までお読みいただきありがとうございました。それでは引き続き次回もよろしくお願いいたします。

一覧に戻る

第4回 深層学習による画像分類

目次